Fractional quantum Hall effect (2): Even-denominator states

It's been procrastinated for a while, more than two months since the first part of this series. I should have finished this post earlier. Now we come to the intriguing part.

In the last post, we talked about the general physics of the integer quantum Hall effect and the fractional quantum Hall effect (FQHE). We ended with a statement regarding the even-denominator FQHE. These are highly nontrivial states that may have great potential in applications, for example, in topological quantum computing. In this post, I will go into more detail about these exotic quantum states and explain why they're special and interesting.

Fig. 1. Even-denominator FQHE in bilayer graphene with paired composite fermions [2]. Illustration from https://nationalmaglab.org/news-events/news/quantum-particle-bilayer-graphene/

Even flux-quanta attachment, that's all?

In the introduction of the FQHE, we have gone through the concept of magnetic flux attachment. We observed that one electron can be grouped with an odd number of quantum fluxes in an FQH state, such as the case of ν = 1/3, where an electron is bound with 2 flux quanta, and the last one is responsible for the Landau quantization of energy. Since a flux quantum is basically a fermion, one electron needs 2n flux quanta to form a composite fermion, and then the physics of QHE follows.

Thus, one expects that at the even-denominator filling factors, which correspond to total even flux quanta, either there's no magnetic flux left for Landau quantization or each electron is attached to an odd number of fluxes forming a composite boson. Neither of these pictures would allow the system to undergo quantum Hall physics by opening a gap in the energy spectrum. Hence, we presume no plateaux of Hall conductance at the even-denominator filling factors such as ν = 1/2, 3/2, 5/2,... But reality turned out to be different!

Fig. 2. Discovery of ν =  5/2 FQHE, W. Pan et al. PRL 83, 17 (1999)

Composite fermions pair up!

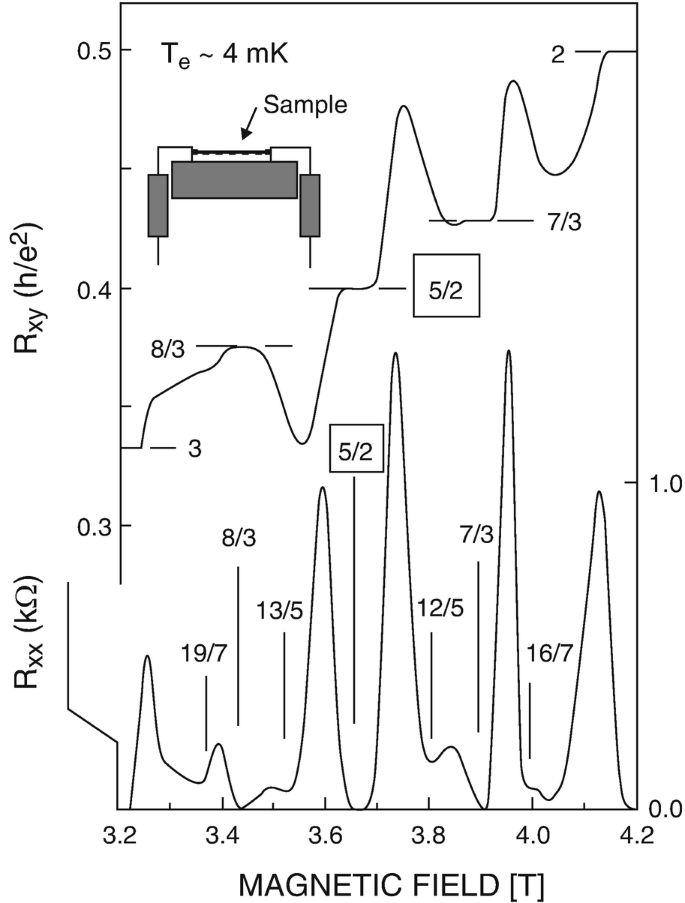
At first, experiments confirmed this prediction for lower filling factors such as 1/4, 1/2..., no plateaux, no gaps. Surprisingly, a robustly exactly flat plateau of Hall conductance, corresponding to a gap similar to that of odd-denominators, appears at ν = 5/2, Fig. 2. This discovery brought the physicists J. Eistentein, M. Heiblum, and J. Jain the 2025 Wolf Prize in Physics. While Eistentein and Heiblum observed in the experiments, Jain explained it beautifully by his own well-established composite fermion picture with a superconducting order. He argues that the gap we see in the ν = 5/2 state is formed when the composite fermions form superconducting pairs. Thus, the role of electron correlation is prone to be critical in an additional layer of physics here. Indeed, theorists have proven that the residual e-e Coulomb interaction after forming composite fermions can be attractive between these newly formed composite particles, facilitating Cooper pair formation within the framework of the BCS theory of superconductivity, Fig. 3. It is noted that FQHE eventually also appears in ν = 1/2 and 1/4, not in normal devices but in special geometry called wide quantum wells.

Fig. 3. Composite fermions pair up in even-denominator filling states, releasing energy and forming a superconducting gap. Figure courtesy: APS/Carin Cain; adapted from M. R. Peterson et al. Phys. Rev. B 82, 235312 (2010)

This theory became very successful in explaining the FQH states in not only the ν = 5/2 state but also recently in wide-quantum well ν = 1/2 and 1/4 states [1], and other states in the lowest Landau level (LLL), such as ν = 3/8, etc. In the ν = 5/2 state, the LLL is filled with both spins, while the 2nd LL is half-filled, see Fig. 4 (A). The filled core levels are irrelevant for low-energy physics, while the half-filled 2nd LL undergoes double-flux attachment and pairing, creating this intriguing physical phenomenon.

Fig. 4 Composite fermion pairing picture of even-denominator FQH states (A) ν = 5/2, where the 'core' levels of the LLL are fully filled as integer QHE, and (B) ν = 3/8, where the 'core' level is the LLL of composite fermions. Figure adopted from C. Wang et al. PNAS 120 (52) e2314212120 (2023)

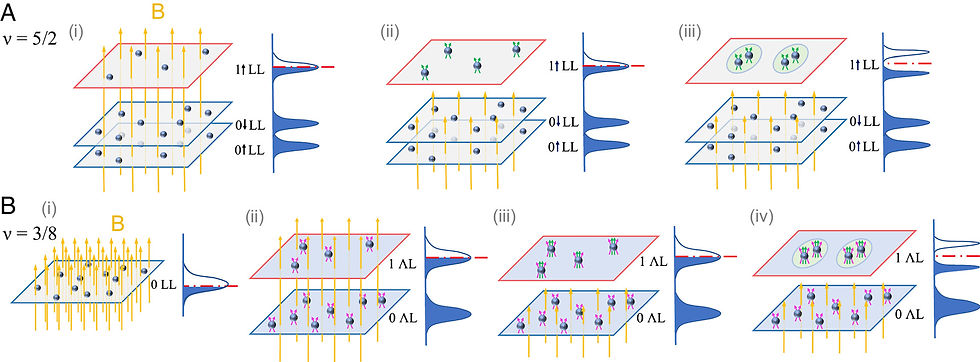
The reason that FQHE does not easily occur in the LLL (such as ν = 1/2 and 1/4 states) stems from the more localized spatial distribution of the composite fermion in the LLL compared to the 2nd LL. In the LLL, Coulomb repulsion is minimized by a more compact distribution (Gaussian shape) of the wavefunction; thus, the normal QHE physics dominates. Whereas, in the 2nd LL, with a broader spread of the wavefunction, Landau energy and residual Coulomb interaction are comparable. And, the latter is strong enough for pairing. Eventually, in higher LLs, Coulomb repulsion grows too strong; it overwhelms Landau energy, and the QHE completely breaks down. We can find an analogy in the distribution of electronic orbitals in the H atom. The LLL resembles 1s orbital, 2nd LL ~ 2s orbital,.... In this very similar manner, the LLL has no node while the 2nd LL has one node at the origin,... (Indeed, the wavefunctions of both LLs and H orbitals are proportional to Laguerre polynomials)

Non-Abelian anyons coming

The intriguing part of physics is not only in how the even-denominator states are formed, it is also in their behaviors. Theoretical works proposed that the ν = 5/2 FQHE must have the p-wave pairing symmetry, similar to the case of ³He superfluid. (It naturally happens that the superconductivity in FQHE should be an odd pairing symmetry state, as we think electrons or composite fermions are all spin aligned, with a magnetic field.) If the readers have already read my earlier post on topological quantum computing and p-wave superconductivity, they would have immediately gotten what I mean by 'intriguing physics' in this case. Indeed, the ν = 5/2 FQHE is another candidate for Majorana fermions and a platform for topological quantum computing.

Fig. 5. A normal quantum vortex (left) and a half-quantum vortex (right). The phase of the superconducting wavefunction only accumulates π around the half-vortex compared to 2π in the normal vortex. These half-quantum vortices were observed in superfluid He-3. Figure from https://physics.aps.org/articles/pdf/10.1103/Physics.9.148

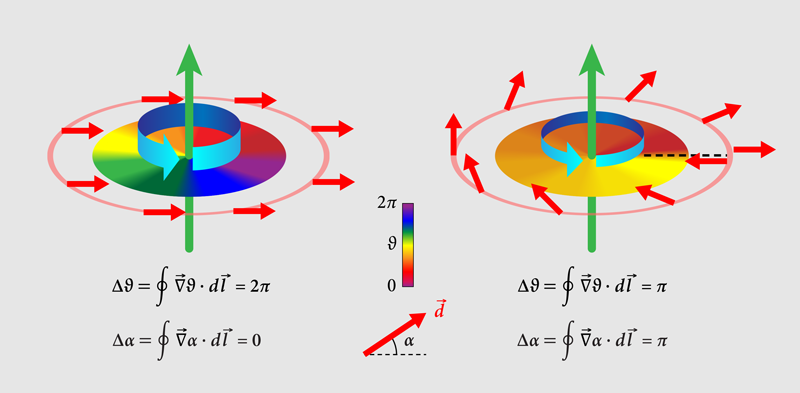
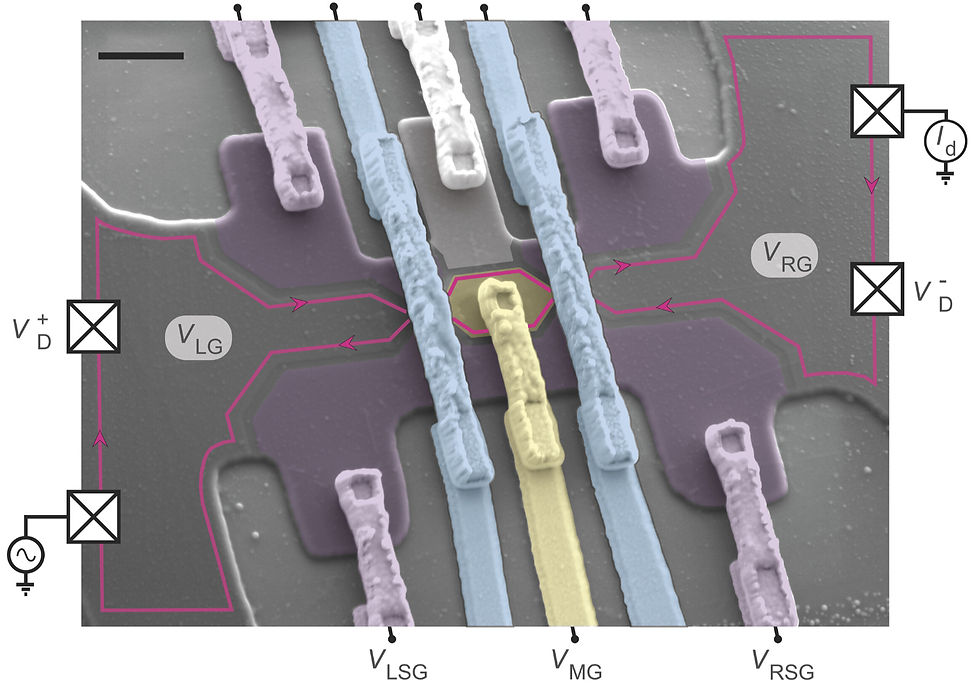
A bit into the technical part of the FQHE non-Abelian anyons, it's more involved with the excitation of the ν = 5/2 FQH state, the quasihole. Remember from the physics of p + ip superconductors, the vortices carry Majorana zero modes. In ν = 5/2 FQHE, the quasiholes are identically the quantum vortices in this special superconducting order. Theory proposes that these vortices carry a quarter of an electron charge (e/4) since a quasihole can split into two, while the effective charge of a composite fermion in the 5/2 state is already only e/2, see Fig. 5. These half-quantum vortices trap Majorana zero modes, and they do all non-Abelian stuff like braiding as I talked about in Topological Quantum Computing. It sounds very promising, but the experimental realization of these phenomena is yet to be done. Even though the braiding of Abelian anyons was realized in ν = 1/3, 2/3 (see Fig. 6), the experiment for the ν = 5/2 seems to be much more challenging!

Fig. 6. A device that scientists realized the braiding experiment of Abelian FQH states in graphene. Figure adopted from T. Werkmeister et al. Science 388, 6748 (2025)

The research on even-denominator FQHE is still very active both in experiments and theory. Some of the results I mentioned above were just done in recent months (by August 2025). We hope to see more advancements in this field ahead, which may lead to more enormous scientific and technical discoveries.

References

1. Composite-fermion pairing at half-filled and quarter-filled lowest Landau level, A. Sharma et al. Phys. Rev. B 109, 035306 (2024)

2. Even-denominator fractional quantum Hall states in bilayer graphene, J. I. A. Li et al. Science 358, 6363 (2017)

3. David Tong notes on QHE: https://www.damtp.cam.ac.uk/user/tong/qhe.html

Bản dịch tiếng Việt (với sự giúp đỡ của chat GPT): Trong bài viết trước, chúng ta đã nói về vật lý tổng quát của hiệu ứng Hall lượng tử nguyên (IQHE) và hiệu ứng Hall lượng tử phân số (FQHE). Chúng ta đã kết thúc bằng một nhận định về các trạng thái FQHE với mức điền có mẫu số chẵn. Đây là những trạng thái phi tầm thường có thể mang tiềm năng to lớn trong các ứng dụng, chẳng hạn như trong tính toán lượng tử tôpô. Trong bài viết này, tôi sẽ đi sâu hơn vào những trạng thái lượng tử kỳ lạ này và giải thích tại sao chúng đặc biệt và thú vị.

Chắp đính lượng tử từ thông chẵn, chỉ vậy thôi sao?

Trong phần giới thiệu về FQHE, chúng ta đã đi qua khái niệm chắp đính từ thông. Ta quan sát thấy một electron có thể được chắp đính với một số lẻ lượng tử từ thông trong một trạng thái FQH, như trường hợp ν = 1/3, nơi một electron gắn với 2 lượng tử từ thông, và lượng tử từ thông cuối cùng chịu trách nhiệm cho sự lượng tử hóa Landau. Vì một lượng tử từ thông về cơ bản là fermion, một electron cần 2n lượng tử từ thông để tạo thành một fermion phức hợp, và từ đó vật lý của hiêu ứng Hall lượng tử (QHE) xuất hiện.

Do đó, chúng ta dự đoán rằng ở các mức điền phân số với mẫu số chẵn, vốn tương ứng với tổng số lượng tử từ thông chẵn, hoặc là không còn từ thông nào để lượng tử hóa Landau, hoặc mỗi electron gắn với số lẻ lượng tử từ thông để tạo thành boson phức hợp. Cả hai cách giải thích này đều không cho phép hệ trải qua quá trình hình thành QHE bằng cách mở vùng cấm trong phổ năng lượng. Vì vậy, ta đoán rằng sẽ không có bậc thang dẫn suất Hall ở các mức điền phân số với mẫu số chẵn như ν = 1/2, 3/2, 5/2,... Nhưng thực tế lại khác!

Fermion phức hợp bắt cặp!

Ban đầu, các thí nghiệm xác nhận dự đoán này cho các phân số nhỏ hơn như 1/4, 1/2..., không có bậc thang Hall lượng tử, không có vùng cấm. Bất ngờ thay, một vùng cấm bền tương tự như ở trường hợp mẫu số lẻ lại xuất hiện ở ν = 5/2. Phát hiện này đã mang về giải thưởng Wolf Vật lý 2025 cho các nhà vật lý J. Eisenstein, M. Heiblum và J. Jain. Trong khi Eisenstein và Heiblum khám phá hiện tượng qua thực nghiệm, Jain đã giải thích nó một cách tuyệt đẹp bằng mô hình fermion phức hợp vốn đã được ông phát triển từ trước với một pha siêu dẫn. Ông lập luận rằng vùng cấm mà ta thấy ở trạng thái ν = 5/2 được hình thành khi các fermion phức hợp ghép cặp siêu dẫn. Do đó, vai trò của tương tác electron trở nên then chốt ở đây. Thật vậy, các nhà lý thuyết đã chứng minh rằng tương tác Coulomb dư giữa các electron, sau khi đã tạo fermion phức hợp, có thể là một tương tác hút đối với những hạt mới này, giúp thúc đẩy sự hình thành cặp Cooper trong khuôn khổ lý thuyết siêu dẫn BCS. Lưu ý rằng FQHE cuối cùng cũng xuất hiện ở ν = 1/2 và 1/4, không phải trong các thiết bị thông thường mà trong hình học đặc biệt gọi là giếng lượng tử rộng.

Lý thuyết này đã trở nên rất thành công trong việc giải thích các trạng thái FQH không chỉ ở ν = 5/2 mà gần đây còn ở các trạng thái ν = 1/2 và 1/4 trong giếng lượng tử rộng [1], và các trạng thái khác trong mức Landau sơ cấp (LLL), như ν = 3/8,... Ở trạng thái ν = 5/2, LLL được lấp đầy cả hai trạng thái spin, trong khi mức Landau thứ cấp chỉ bị điền một nửa, xem Hình 4(A). Các mức lõi đã lấp đầy hoàn toàn nên không liên quan đến các hiệu ứng vật lý năng lượng thấp, trong khi mức Landau thứ cấp được bán điền, chắp đính từ thông, rồi ghép cặp, tạo nên hiện tượng vật lý thú vị này.

Nguyên nhân FQHE không dễ xảy ra ở LLL (như các trạng thái ν = 1/2 và 1/4) bắt nguồn từ phân bố không gian tập trung hơn của fermion phức hợp ở LLL, so với mức Landau thứ cấp. Trong LLL, lực đẩy Coulomb được giảm thiểu nhờ phân bố gọn hơn (dạng Gaussian) của hàm sóng; do đó, vật lý Hall lượng tử bình thường chiếm ưu thế. Trong khi đó, ở mức Landau thứ cấp với sự trải rộng hơn của hàm sóng, năng lượng Landau và tương tác Coulomb dư là tương đương nhau, và tương tác Coulomb này đủ mạnh để ghép cặp các fermion phức hợp. Cuối cùng, ở các mức Landau cao hơn, lực đẩy Coulomb trở nên quá mạnh, áp đảo năng lượng Landau, và vật lý Hall lượng tử hoàn toàn bị phá vỡ. Ta có thể tìm thấy sự tương tự trong trường hợp phân bố orbital điện tử của nguyên tử H. LLL giống orbital 1s, mức Landau thứ cấp ~ 2s,... Tương tự như vậy, LLL không có nút, trong khi mức Landau thứ cấp có một nút tại gốc,... (Thật vậy, hàm sóng của cả mức Landau và orbital H đều tỉ lệ với đa thức Laguerre).

Anyon phi giao hoán tính

Điều hấp dẫn trong vật lý của FQHE không chỉ nằm ở cách các trạng thái mẫu số chẵn được hình thành, mà còn ở tính chất của chúng. Các công trình lý thuyết đề xuất rằng FQHE ở ν = 5/2 phải có đối xứng ghép cặp hàm p, tương tự trường hợp He-3 siêu lỏng. (Ta có thể thấy điều này xảy ra một cách tự nhiên rằng siêu dẫn trong QHE phải có đối xứng lẻ, do điện tử hoặc fermion phức hợp đều có cùng phân cực spin dưới từ trường.) Nếu độc giả đã đọc bài trước của tôi về điện toán lượng tử tôpô, siêu dẫn hàm p, các bạn sẽ lập tức nhận ra điều tôi gọi là “điều kì thú” của hiện tượng này. Đúng vậy, FQHE ở mức ν = 5/2 là một ứng cử viên để tạo ra hạt Majorana, nền tảng cho điện toán lượng tử tôpô.

Một chút về phần kỹ thuật của anyon phi giao hoán tính trong FQHE: nó liên quan nhiều đến kích thích của trạng thái FQH ν = 5/2, tức các chuẩn hốc (quasihole, phần còn lại khi ta lấy đi một chuẩn hạt, quasiparticle, trong một hệ). Ta nhớ lại từ vật lý của siêu dẫn hàm p + ip, các xoáy lượng tử mang các mức không Majorana ở lõi của chúng. Trong FQHE ν = 5/2, các chuẩn hốc chính là các xoáy lượng tử trong pha siêu dẫn này. Ta có thể chứng minh rằng các xoáy này mang 1/4 điện tích của một điện tử (e/4) vì biểu diễn toán học chỉ ra rằng một chuẩn hốc có thể tách thành hai, trong khi điện tích hiệu dụng của một fermion phức hợp ở mức điền ν = 5/2, tương tự ν = 1/2 vốn chỉ là e/2, xem Hình 5. Vì vậy chúng được gọi là bán xoáy lượng tử. Những bán xoáy lượng tử này giữ các mức không Majorana và thực hiện tất cả tính chất phi giao hoán tính như bện lượng tử mà tôi đã nói trong bài về điện toán lượng tử tôpô. Nghe có vẻ đầy hứa hẹn, nhưng việc hiện thực hóa thí nghiệm của những hiện tượng này vẫn chưa được thực hiện. Dù bện anyon giao hoán tính đã được thực hiện ở ν = 1/3, 2/3 (Hình 6), nhưng thí nghiệm cho ν = 5/2 dường như khó khăn hơn nhiều!

Nghiên cứu về FQHE mẫu số chẵn vẫn đang rất sôi động cả trong thí nghiệm lẫn lý thuyết. Một số kết quả tôi đề cập ở trên chỉ mới được công bố trong vài tháng gần đây (Tháng 8, 2025). Chúng ta hy vọng sẽ thấy nhiều bước tiến hơn trong lĩnh vực này, có thể dẫn đến những khám phá khoa học và kỹ thuật to lớn hơn.