Emergent quantum geometry in solids

Quantum geometry is not a new concept in physics; it was first proposed in the 1980s by mathematical physicists. This framework found early applications in atomic physics, particularly in the study of two-level systems, which are foundational to the field. Recently, quantum geometry has attracted significant attention in condensed matter physics. Closely tied to topological physics, it extends the mathematical toolkit of physics from topology to geometry.

In this blog, I will provide a concise introduction to quantum geometry—specifically quantum metrics—and discuss their role in exploring both new and established physical phenomena. Additionally, I have included the presentation slides from my talk at the Quantum-material Interdisciplinary Research Exchange (QuIRE) seminar at UChicago in June 2024, which are available at the end of this article.

To understand quantum geometry, we must first grasp the concept of a Hilbert space. In quantum mechanics, a Hilbert space represents the space of all possible quantum states of a system. Rather than delving into its rigorous mathematical definition, I will explain it in an intuitive way for physics learners.

In physics, we often describe a system using either a Lagrangian or a Hamiltonian. While Lagrangians are commonly used in field theories, Hamiltonians are particularly useful in quantum mechanics because they can be represented as matrices. In essence, solving a quantum mechanics problem often involves linear algebra: diagonalizing a matrix to find its eigenstates and corresponding eigenvalues.

The Hilbert space is the mathematical structure spanned by these eigenstates, which serve as its basis. This space encapsulates all the information about a quantum system, and the evolution or behavior of the system can be tracked by how its states change within this space.

Quantum geometry is the study of the geometric properties of the Hilbert spaces associated with quantum mechanical systems. It can be analogized to Einstein's theory of General Relativity, which examines the geometry of spacetime, how it is deformed by gravity, and how this deformation influences the motion of objects. Similarly, quantum geometry explores how the states of a quantum system—represented within the Hilbert space—behave and interact.

One striking example of quantum geometry in action is the nonlinear Hall effect observed in many materials. Unlike the conventional Hall effect, where the Hall response depends linearly on the applied current, the nonlinear Hall effect involves higher-order dependencies, offering new insights into the interplay between quantum geometry and material properties.

Fig. 1. The effect of quantum geometry on electronic states is similar to that of spacetime on light according to general relativity. Figure credit: Nat. Phys. 20, 1110 (2024)

Once the geometry of a quantum system is defined, it becomes possible to calculate quantum distances in its parameter space. This parameter space refers to the parameterized Hilbert space, which contains all the accessible information about the system. For instance, in condensed matter physics, the Brillouin zone serves as the parameter space for Bloch states, with crystal momentum k acting as the parameters. Similarly, in a two-level system, the Bloch sphere represents the Hilbert space, parameterized by external applied fields. These examples illustrate how parameter spaces provide a geometric framework for understanding quantum systems. The quantum distances are the distances between states in these spaces.

Fig. 2. Quantum distances ds^2 in (A) a Brillouin zone (B) in a Bloch sphere.

This quantum distance turns out to be proportional to the variance of the parameters multiplied by a factor matrix Q, called a quantum geometric tensor. This tensor governs the geometric and topological properties of the Hamiltonian. Its real part is the quantum metric (to measure the distance in Hilbert space) and the imaginary part is the Berry connection whose curvature is famous in topological physics. (Please see the attached slides for the formal derivation of these quantities.)

The Berry curvature accumulated along a closed loop in parameter space is proportional to the integer-valued Chern number. This topological quantity underpins several anomalous phenomena in physics, including the anomalous Hall effect, circular photogalvanic effect, quantum spin Hall effect, and the behavior of topological insulators. In contrast, the quantum metric—another geometric property of the parameter space—plays a key role in phenomena such as the nonlinear Hall effect. Interestingly, recent studies have identified materials like MnBi2​Te4​ and Mn3​Sn that exhibit the nonlinear Hall effect even in the absence of Berry curvature.

Moreover, the quantum metric contributes to superconductivity in ultra-flat-band systems, such as twisted bilayer graphene. By effectively giving mass to Cooper pairs, the quantum metric facilitates the emergence of a superfluid phase, making superconductivity possible. (For further details, refer to the presentation slides attached.)

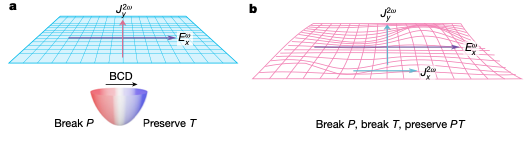
Fig. 3. The Hilbert space with both inversion (P) and time-reversal (T) symmetries broken but PT preserved (right) compared with one having broken P only (left), the Berry curvature vanishes and the quantum metric induces the anomalous Hall effect. Figure credit: Nature 621, 487-492 (2023)

References:

Quantum Geometric Tensor (Fubini-Study Metric) in Simple Quantum System: A pedagogical Introduction, arXiv:1012.1337

Nat. Mat. 20, 1601 (2021)

Annu. Rev. Condens. Matter Phys. 12, 247–272 (2021)

Nature 621, 487–492 (2023)

PRL 132, 026301 (2024)

Nat. Phys. 20, 1110 (2024)

An interesting essay on quantum geometry: Essay: Where Can Quantum Geometry Lead Us? Päivi Törmä, PRL 131, 240001 (2023)

QuIRE_0625.pdf

Download PDF • 25.61MB