[Vietnamese version] Hình học lượng tử xuất hiện trong chất rắn

Hình học lượng tử không phải là một khái niệm mới trong vật lý; nó được các nhà lý toán học đề xuất lần đầu vào những năm 1980. Khung lý thuyết này đã sớm được ứng dụng trong vật lý nguyên tử, đặc biệt là trong nghiên cứu các hệ hai mức, vốn là nền tảng của lĩnh vực này. Gần đây, hình học lượng tử đã thu hút sự quan tâm đáng kể trong vật lý vật chất ngưng tụ. Liên kết chặt chẽ với vật lý tôpô, nó mở rộng bộ công cụ toán học của vật lý từ tôpô sang hình học.

Trong bài viết này, tôi sẽ giới thiệu ngắn gọn về hình học lượng tử—cụ thể là quy độ lượng tử (quantum metric)—và thảo luận về vai trò của chúng trong việc khám phá cả những hiện tượng vật lý mới và đã được biết đến. Ngoài ra, tôi cũng đã đính kèm bài thuyết trình của mình tại seminar Quantum-material Interdisciplinary Research Exchange (QuIRE) tại Đại học Chicago vào tháng 6 năm 2024, có sẵn ở cuối bài viết này.

Giới thiệu về không gian Hilbert

Để hiểu hình học lượng tử, trước tiên chúng ta cần nắm bắt khái niệm về không gian Hilbert. Trong cơ học lượng tử, không gian Hilbert biểu diễn không gian của tất cả các trạng thái lượng tử có thể có của một hệ. Thay vì đi sâu vào định nghĩa toán học chặt chẽ, tôi sẽ giải thích theo cách trực quan cho những người học vật lý.

Trong vật lý, chúng ta thường mô tả một hệ thống bằng hàm Lagrange hoặc toán tử Hamilton. Các hệ vật lý tuân theo nguyên lý tác dụng tối thiểu (thông qua hàm Lagrange) theo phương trình Euler-Lagrange (xem thêm cơ học Lagrange), còn toán tử Hamilton, trong cơ học lượng tử, tác dụng lên hàm sóng của một hệ cho ra tổng năng lượng của nó. Trong khi hàm Lagrange thường được sử dụng trong lý thuyết trường, toán tử Hamilton đặc biệt hữu ích trong cơ học lượng tử vì chúng có thể được biểu diễn dễ dàng dưới dạng ma trận. Về bản chất, giải một bài toán cơ học lượng tử thường liên quan đến công việc của đại số tuyến tính: chéo hóa một ma trận để tìm các trạng thái riêng và giá trị riêng (chính là các mức năng lượng) của nó.

Không gian Hilbert là cấu trúc toán học được tạo ra từ các trạng thái riêng này, đóng vai trò là cơ sở của không gian đó. Toàn bộ thông tin về một hệ lượng tử được mã hóa trong không gian Hilbert, và sự biến đổi hoặc tương tác của hệ có thể được theo dõi bằng cách nghiên cứu sự thay đổi của các trạng thái trong không gian này.

Hình học lượng tử là gì?

Hình học lượng tử là nghiên cứu về các tính chất hình học của không gian Hilbert liên quan đến các hệ cơ học lượng tử. Nó có thể được so sánh với Thuyết tương đối rộng của Einstein, trong đó hình học của không-thời gian bị biến dạng bởi lực hấp dẫn và sự biến dạng này ảnh hưởng đến chuyển động của vật thể. Tương tự, hình học lượng tử khám phá cấu trúc hình học của không gian Hilbert, cách các trạng thái của một hệ lượng tử—được biểu diễn trong không gian này—biến đổi và tương tác với nhau.

Một ví dụ nổi bật về hình học lượng tử trong thực tế là hiệu ứng Hall phi tuyến được quan sát trong nhiều vật liệu. Khác với hiệu ứng Hall thông thường, trong đó hiệu điện thế Hall tỷ lệ tuyến tính với cường độ dòng điện áp dụng, hiệu ứng Hall phi tuyến liên quan đến các bậc cao hơn, cung cấp những hiểu biết mới về mối quan hệ giữa hình học lượng tử và tính chất vật liệu.

Hình 1. Tác động của hình học lượng tử lên trạng thái điện tử tương tự như ảnh hưởng của không-thời gian lên ánh sáng theo thuyết tương đối rộng. Figure credit: Nat. Phys. 20, 1110 (2024)

Khoảng cách lượng tử và tensor hình học lượng tử

Khi hình học của một hệ lượng tử được xác định, chúng ta có thể tính khoảng cách lượng tử trong không gian tham số của nó. Không gian tham số này là không gian Hilbert có tham số hóa, chứa tất cả thông tin về hệ thống.

Ví dụ:

• Trong vật lý vật chất ngưng tụ, vùng Brillouin đóng vai trò là không gian tham số cho các trạng thái Bloch, với động lượng tinh thể k là tham số.

• Trong một hệ hai mức, mặt cầu Bloch biểu diễn không gian Hilbert, được tham số hóa bởi các trường ngoài tác dụng lên hệ.

Hình 2. Khoảng cách lượng tử ds² trong (A) vùng Brillouin và (B) mặt cầu Bloch.

Khoảng cách lượng tử này tỷ lệ thuận với bình phương biến thiên của các tham số, nhân với một ma trận (tenxơ) Q gọi là tenxơ hình học lượng tử. Tenxơ này chi phối các tính chất hình học và tôpô của toán tử Hamilton đang xem xét:

• Phần thực của nó là quy độ lượng tử (quantum metric), dùng để đo khoảng cách trong không gian Hilbert.

• Phần ảo của nó là liên độ Berry (Berry connection), có khúc suất Berry (Berry curvature) nổi tiếng trong vật lý tôpô.

Số Chern, một đại lượng tôpô quan trọng, được tính bằng khúc suất Berry tích lũy theo một vòng kín trong không gian tham số. Số Chern là nền tảng của nhiều hiện tượng vật lý bất thường, chẳng hạn như:

• Hiệu ứng Hall dị thường (lượng tử) ((quantum) anomalous Hall effect)

• Hiệu ứng quang điện động lượng tử (quantum photogalvanic effect)

• Hiệu ứng Hall spin lượng tử (quantum spin Hall effect)

• Tính chất của các chất cách điện tôpô

• Hiệu ứng Hall (dị thường) phi tuyến (nonlinear (anomalous) Hall effect).

Trong khi đó, quy độ lượng tử—một tính chất hình học khác của không gian tham số—đóng vai trò quan trọng trong các hiện tượng như hiệu ứng Hall phi tuyến. Điều thú vị là một số vật liệu như MnBi₂Te₄ và Mn₃Sn thể hiện hiệu ứng Hall phi tuyến ngay cả khi không có khúc suất Berry [4, 6]. Việc khúc suất Berry dẫn tới hiệu ứng Hall phi tuyến đã được biết tới trước đó, nhưng ở những vật liệu này, các nhà khoa học đã thiết kế các thí nghiệm làm cho khúc suất Berry tiêu biến thông qua phá vỡ cả đối xứng chẵn lẻ (P) và đối xứng thời gian nghịch đảo (T) nhưng lại bảo toàn đối xứng hợp PT. Việc quan sát được hiệu điện thế Hall phi tuyến đã khẳng định nguyên nhân duy nhất là quy độ lượng tử.

Hơn nữa, quy độ lượng tử còn góp phần vào hiện tượng siêu dẫn trong các hệ dải phẳng (flat band) siêu mỏng như graphene xoắn hai lớp [7]. Bằng cách tạo khối lượng hiệu dụng cho các cặp Cooper, quy độ lượng tử thúc đẩy sự hình thành pha siêu lỏng, giúp siêu dẫn xảy ra.

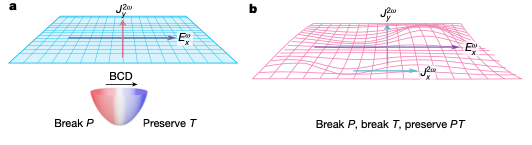
Hình 3. Không gian Hilbert với đối xứng nghịch đảo (chẵn lẻ) (P) và nghịch đảo thời gian (T) bị phá vỡ nhưng đối xứng PT được bảo toàn (hình bên phải) so với trường hợp chỉ đối xứng P bị phá vỡ (hình bên trái). Trong trường hợp này, khúc suất Berry triệt tiêu và quy độ lượng tử gây ra hiệu ứng Hall dị thường. Figure credit: Nature 621, 487-492 (2023)

Tài liệu tham khảo:

[1] Quantum Geometric Tensor (Fubini-Study Metric) in Simple Quantum System: A pedagogical Introduction, arXiv:1012.1337

[2] Nat. Mat. 20, 1601 (2021)

[3] Annu. Rev. Condens. Matter Phys. 12, 247–272 (2021)

[4] Nature 621, 487–492 (2023)

[5] PRL 132, 026301 (2024)

[6] Nat. Phys. 20, 1110 (2024)

[7] Nature 614, 440–444 (2023)

[8] An interesting essay on quantum geometry: Essay: Where Can Quantum Geometry Lead Us? Päivi Törmä, PRL 131, 240001 (2023)

QuIRE_0625.pdf

Download PDF • 25.61MB